Color Measurement in Coating, Plastic, Textile and Food Industries

In the painting and coating industry as well as in the textile and plastic industries colorimeters have been in use for many years. The processing industries are discovering the advantage of colorimeters more and more. Colorimeters have a favorable effect on production monitoring and quality control.

Judging colors is a very subjective matter. Moreover one cannot sense colors with the same sensitivity everyday. Sometimes they are more or sometimes less differentiated. The usage of colorimeter allows an objective control of colors. This is especially required when different suppliers have to provide components of the same color. Colorimeters are available for various purposes and requirements in different categories and different price ranges.

Individual coordinated colorimeters are offered for different, industrial requirements.
The following colorimeters permit - unless differently specified - both an absolute difference and a measuring difference for various colorimetric systems:

In addition, white and yellow degrees according to ASTM E313-98 and the metamerism index according to DIN 6172 can be determined.

All described colorimeter can be connected to a computer with the operating system of Windows and they can also be controlled by it. Either it is connected through the serial interface or via a USB port. You cannot only store color standards, but also the color standard’s individual pass/fail tolerances. This is a very important criterion because there are no universal color tolerances.

The relative acceptable tolerance size depends on several factors. Several factors are, for example, color, materials or surface texture, but also the application area of the colored product or the customer requirements. Everyone who is using color measuring technologies in quality control, is recommended, to determine pass/fail patterns after visual aspects considering its own individual requirements. Then the samples should be measured. Resulting color distances to the origin pattern form the tolerances that are deposited in the  colorimeter.

Colorimetry allows a consistent quality by objective examination, also of different people. The main difference between the different devices is the measuring geometries. On the one hand there are  devices that illuminate the sample with diffuse light and measure the reflected light at an angle of 8° and on the other hand, those which bring an adjusted ray under 0° (vertical) to the sample and measure the light  eflected under 45°.

The d:8° measuring geometry (diffused light) is popular primarily in the painting and coating industry. This measuring method is particularly an advantage when comparing patterns with differentiated surface conditions (such as gloss) regarding to the hue but the surface effects disarrange the results of the color measurement.

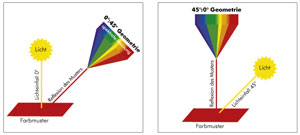The 0°/45° measuring geometry is particularly suitable for high-gloss surfaces, for matte textile patterns and when it comes to the point, to achieve visual optimal matching.

CIE Color Spaces
Founded in 1931, the CIE Commission Internationale de l'Eclairage, International Lighting Commission, is responsible for monitoring and reviewing all progress in quantifying (establishing internationally accepted values) of color.
Standardized color measurement systems are the basis of modern color communication. They make it possible to describe the three attributes of a color hue - brightness - saturation with numerical values. With these values, each color can be assigned a color location in the respective color space. The CIE defines: light sources as types of light, objects as spectral data, observer by observer function.

Color spaces are a mathematical construct. All visible, for the human being perceptible colors have a space called color space in three dimensional unlimited color spaces.

The Color spaces can be colored only with dyes and pigments. All actually colored, physical color patterns of the color systems form a limited color space. All colors that are outside this limit cannot be displayed as a color sample.

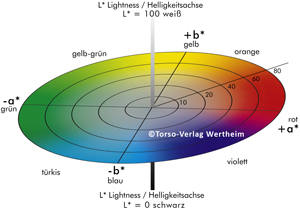The L*a*b* color space of 1976
The L*a*b* color space, also known as the CIELAB system, is still the most commonly used system for colorimetry today. It was defined as an equidistant color space by the CIE in 1976, and is easier to understand by the three-dimensional representation than the x y-coordinate plot in the shoe sole diagram.

Strictly speaking, the CIELAB system is not evenly spaced, but it provides a good match of perceived and measured color spaces. The simple structure of the color space through three independent color values ​​persuades to the present day and leaves little chance to more precise, but in some cases far more complicated systems.
The color space is defined by the vertical L*-axis, which is a measure of the brightness of the color, and the axes a * and b * arranged at right angles to it.
The ends of the axes symbolize the six primary colors red, green, blue, yellow, black and white. The a*-axis extends from its positive strand over the zero point to its negative strand from red to green, the b*-axis correspondingly from yellow to blue. The L*-axis starts at 0 with black and goes up to 100 which stands for an idealized white.
So a* and b* span the color plane, which is not colored in the middle (white, gray or black, depending on the brightness). Outwardly there is no demarcation. The more the values ​​of a* and b* differ from zero (that is, in both the positive and negative directions), the greater the Chroma of the color.
The representation of a geometric body, the color body, always refers to certain specifications. Thus, the image of the RAL Design color body shows the colors realized in this system.

Lab without CIE or * label describe the Hunter Lab.
The Hunter Lab color space was developed in 1948 by R. S. Hunter. It is similar but not identical to the L*a*b* of the CIE and is still used in some areas.

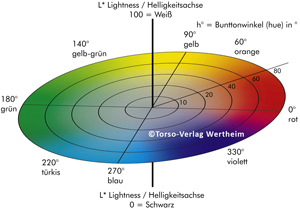The L*C*h* color space
The color space spanned by the orthogonal axes L*, a* and b* can also be described in an alternative way. In mathematics, there are not only right-angled coordinate systems, the so-called Cartesian, but also the cylindrical coordinate systems. So also the color space and the points in this space, so the colors, can be described with cylindrical coordinates. The vertical orientation here is also the brightness axis L*, identical to L* from the L*a*b* color space. The horizontal extent of the space is described by the vector C* and the angle h*, which - if only the plane is considered - are also called polar coordinates. The length of the vector C*, which starts from the axis L*, corresponds to the distance of the color from the neutral gray axis in the center of the cylinder. The angle h* describes the position of the vector C* in the plane, which extends 360 ° around the vertical L * axis.
As complicated as this seems at first sight, the more logical attributes are the hue, brightness, and Chroma attributes assigned to the mathematical terms h*, L*, and C*. The possible hues occur very often in the representation of a color wheel. Thus, the term hue quickly loses its mathematical horror. By convention, 0° or 360° is red (+ a), 90° is yellow (+ b), 180° is green (-a) and 270° is blue (-b). The brightness L* increases from bottom to top and can take values ​​from 0 to 100 - at least theoretically. The chroma C* may vary depending on the hue, depending on light and dyes or pigments take different maximum values, there is no demarcation here.

The RAL Design System is a coloration of the coordinates h* L* C* and a look into the color atlas makes the contexts immediately clear.
The abbreviations h* L* C* are based on the English terms for hue, brightness and chroma: Hue, Lightness and Chroma.

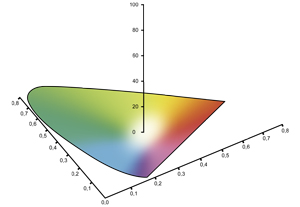The color space xyY - the standard color chart
The standard color chart, also known as "shoe sole", is used and illustrated very often and serves to define color specifications and color ranges, especially in DIN regulations. It is the least vivid way to define colors.
In a diagram, the standard color value components x and y are entered as coordinates. If this is done for all visible colors, the diagram has the typical shoe sole shape. In its center is the point that corresponds to a uniform excitation of all three types of cones and reflects no color. At the edges, the colors are more intense, on the edge of the shoe sole are the strongest. On the curved curve are also the spectral colors (sort of pure colors), which is why the "edge" is also called Spektralfarbenzug. The connection of the two ends is called Purpurgerade, spectral colors do not exist here.

But where do the standard color value components come from?
The standard color values ​​X, Y and Z result from the interaction of the light reflected by a colored object with the three color-sensitive cones of the human eye. In the colorimetry, the tristimulus process mirrors exactly this process, the task of the cones is taken over here by appropriate filters.
X, Y, Z are a measure of the irritation of the red, green, blue-sensitive cones.
X, Y, Z represent the red, green, and blue portions of the colored light reflected from the object.
The standard color value shares result as the ratio of a standard color value to the sum of all three standard color values:
In the two-dimensional plot of x and y all colors can be described, but there is no distinction according to different brightness. Since the green sensitivity of the eye is almost parallel with the light sensitivity, Y is also used as a measure of the brightness. Thus, the representation of all possible colors in a xyY arrangement is possible, but rarely used.

In the definition of colors, the specification of x and y values ​​or the entry of points or areas in the shoe sole is not sufficient. In addition, an indication of the brightness, ie the order of Y is necessary.

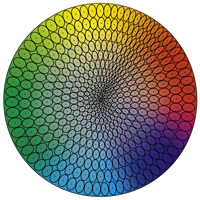CMC color tolerance space
The formula named after the Color Measurement Committee in the United Kingdom leads to a specific weighting of individual differences before calculating the total color distance. In this case, the ratio of the weighting of brightness and Chroma to each other can be freely selected. Example textile industry: ratio 2: 1. The color difference in this case is called dE CMC (2: 1).
Depending on this ratio, the tolerance range can be a sphere (1: 1) or an Ellisoid (from 1.1: 1). As the ratio increases, the expansion of the sphere increases accordingly. The ratio L: c is also called Commercial Factor (cf). Advantage of dE CMC: Definition of a tolerance value for all color ranges!

Color distance calculations

The calculation of the color distance dE over L * a * b * or h * L * C * leads to quantities that do not always agree with the visual evaluation. This is because these color spaces are only approximately equidistant. The requirement for equidistance is the requirement to arrange the colors in such a way that equally large visual color differences also correspond to equally large mathematical values ​​for the color difference.
To match the calculated color differences to human sensations, various formulas have been developed. The best known is the so-called CMC formula.

Color tolerances

• Set color tolerance values ​​based on visual criteria
• Perception of the color difference, especially in the hue, then in the chroma and finally in the brightness
• Do not set the same tolerance for all colors
• Total tolerance dE, but better set individual tolerances for dL *, da * and db *
• Tolerances that are smaller than the visually detectable differences or the measuring device match make no sense!

• Visual color matching with natural and artificial daylight with description of the necessary types of light, observation geometry and lighting geometry, the lighting conditions and the visual properties of the observer.
• Application of color measurement with a description of the sample properties, the illumination geometries and measurement geometries and the specifics of samples such. Metallics, fluorescence and thermochromy.
• Explanation of the CIELAB color system and the CIELAB formula with reference to DIN 5033 and DIN 6174 and the CIELAB color space formula ΔE * ab
• Significance of color differences, i.e. check whether a measured or graded color difference actually exists or was caused by procedural errors.
• Tolerance determination and tolerance agreement based on the fact that the human eye is better able to recognize color differences in the achromatic color range than in the saturated range.
• Testing the color of colorants, including relevant raw materials such as pigments of printing inks, colored pigments, white-based, black pigments, metallic paints and pearlescent, and methods therefor with reference to literature and DIN standards.
• User-specific questions on the topics of paints and emulsion paints, printing inks, plastics, textiles with references to relevant literature.

The DIN Technical Report 49 offers a practical introduction to color quality testing with practical reference and references to accompanying literature and the necessary DIN standards.
The DIN Technical Report 49 is available from Beuth-Verlag at www.beuth.de